결합분포 (joint distrbution)
- 이제까지는 한 번에 하나의 변수만을 다루는 방법에 대해 살펴보았다
- 이제부터는 두 변수 사이의 상호관계를 분석하기 위한 방법을 살펴본다
- 남녀간의 관계처럼 많은 경우 둘 간의 관계가 중요하다
- 예: 교육과 임금
- 예: 통화증가율과 물가상승률
- 예: 학급 규모와 학생 성적
- 결합분포 : 두 변수 간의 관계 전모를 보여줌
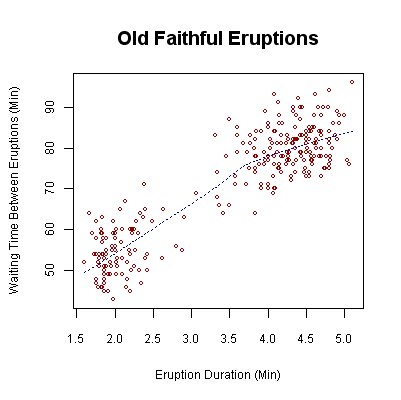
산포도 (scatter plot)
- 두 변수 사이의 관계를 살펴보기 위해 산포도를 이용한다.
- 설명변수는 x로 표기하고 가로축에 표시
- 피설명변수는 y로 표기하고 세로축에 표시
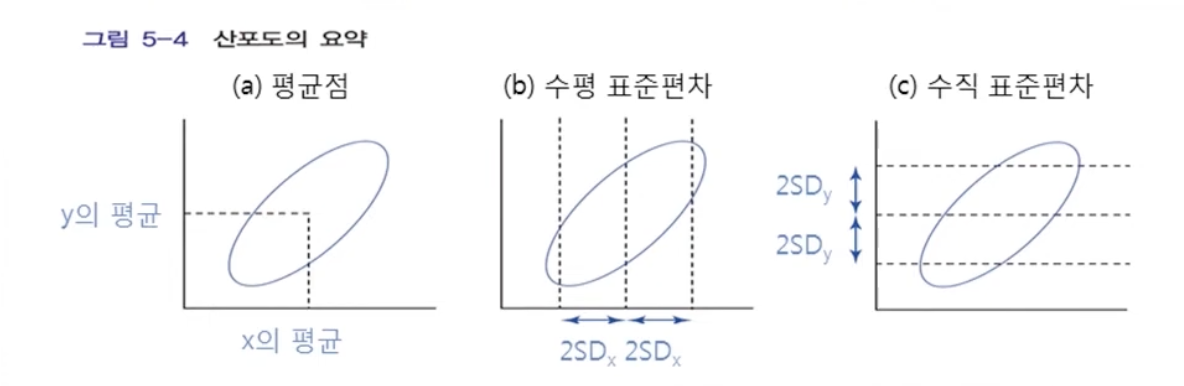
산포도의 요약
- 가로로 보면 대략 95%의 점들이 x 평균점을 기준으로 $ \pm 2SD_{x}$ 이내에 위치함
- 세로로 보면 대략 95%의 점들이 y 평균점을 기준으로 $ \pm 2SD_{y}$ 이내에 위치함
- x의 평균과 표준편차, y의 평균과 표준편차는 x 와 y의 분포를 따로따로 요약
상관계수의 필요성
- 가로든 세로든 평균과 표준편차가 동일해도 두 변수의 관계는 상이
- 위의 산포도 좌측 3개씩 6개를 보면 가로든 세로든 중심과 퍼진 정도가 동일하지만 좌측으로 갈수록 더 강한 선형관계를 보임
- 두 변수간 선형관계의 방향과 강도가 얼마나 되는지 측정할 필요성 대두
- 상관계수는 두 변수가 선형관계의 방향과 강도 측정
두 변수 사이의 관계를 보는 3가지 키워드 : 선형 관계 , 방향 (+/-로 확인 가능) , 강도 (절대값이 1에 가까울수록 선형이다)
이변량 자료의 요약 통계량
- x의 평균과 표준편차
- y의 평균과 표준편차
- x와 y간 상관계수
상관계수의 범위, 부호
- 범위 : $-1\leq r \leq 1$
- 상관계수 = 1 또는 -1 아니면 완전상관 (perfect correlation)
- 모든 점들이 정확히 하나의 선 위에 위치
- 양의 상관관계이면 점의 분포가 우상향
- 음의 상관관계이면 점의 분포가 우하향
- 두 변수의 표준편차가 모두 0이면 상관계수를 정의할 수 없음
- 두 변수 중 어느 한 변수만의 표준편차가 0이면 상관계수는 0
상관계수 구하는 절차 1
$r=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{\sum_{n}^{i=1}(x_{i}-\overline{x})^2} \sqrt{\sum_{n}^{i=1}(y_{i}-\overline{y})^2}}$
1) 각 변수를 평균으로부터의 편차로 바꾼다.
2) 두 편차를 서로 곱한 뒤 합친다.
3) 각 편차를 제곱하여 합치고, 다시 제곱근을 취한다. 두 제곱근을 곱한다.
4) 위 2)에서 얻은 값을 위 3)에서 얻은 값으로 나눈다.
상관계수 구하는 절차 2
(변형된 공식)
$
r = \frac{\sum_{i=1}^{n} \frac{(x_i - \bar{x})(y_i - \bar{y})}{n-1}}
{\sqrt{\sum_{i=1}^{n} \frac{(x_i - \bar{x})^2}{n-1} \sum_{i=1}^{n} \frac{(y_i - \bar{y})^2}{n-1}}}
$
1) 각 변수를 평균으로부터의 편차로 변환한다.
2) 두 편차를 서로 곱하여 합친 뒤 자유도 $n-1$ 로 나누어 공분산을 구한다.
3) 두 표준편차를 곱한다.
4) 위 2)에서 구한 값을 위 3)에서 구한 값으로 나눈다.
분모 : x와 y 각각의 표준편차의 곱
분자 : "공분산 (covariance)"
공분산 (Covariance)
- X 편차와 Y 편차들의 곱의 대략적인 평균이다
- 산포도를 다시 생각해보자.
- x와 y의 상관계수가 + 일 때, 공분산도 + 겠다!
- 상관계수의 부호는 공분산의 부호가 반영이 될것이다.
- 분모는 무조건 + 이기 때문
그렇다면 왜 공분산이 아니라 상관계수로 보는가?
- 상관계수를 단위와 관계 없이 독립적으로 정의하기 위함!
- 키와 몸무게의 상관관계를 구한다면, 공분산으로만 얘기하면 키를 m, cm 등등 어떻게 재느냐에 따라 값이 달라진다.
- 공분산의 단위의 의미를 없애기 위하여 상관계수를 활용한다.
- -1 ~ 1의 구간을 갖기에 단위에 상관없이 판단이 가능하다
상관계수의 해석
- 상관계수의 의미
- '상관계수 = 0.8'은 산포도 상에서 80%의 점들이 하나의 선 주위에 빽빽하게 밀집해 있다는 것을 의미하지 않는다.
- '상관계수 = 0.8'은 상관계수가 0.4일 때보다 선형관계의 강도가 강하기는 하지만 정확히 두 배로 강하다는 것을 의미하지도 않는다.
- 산포도상에서 표준편차를 변화시킬 때의 시각적 효과

상관계수가 유용하지 않은 경우
- 이탈값 (outlier)이 존재하는 경우
- 두 변수가 관계가 비선형인 경우
- 상관계수가 0이 나왔다고 하여, 관계가 없음을 의미하지 않는다
- 선형 관계가 아닐 뿐 다른 관계는 있을 수 있다!
변수 변환
- 적절한 변수변환을 통하여 비선형 관계를 선형관계로 근사시킴
- 예) (x, y)간 존재하는 원래의 비선형 관계가 (x, ln(Y))간 선형관계로 바뀐 경우
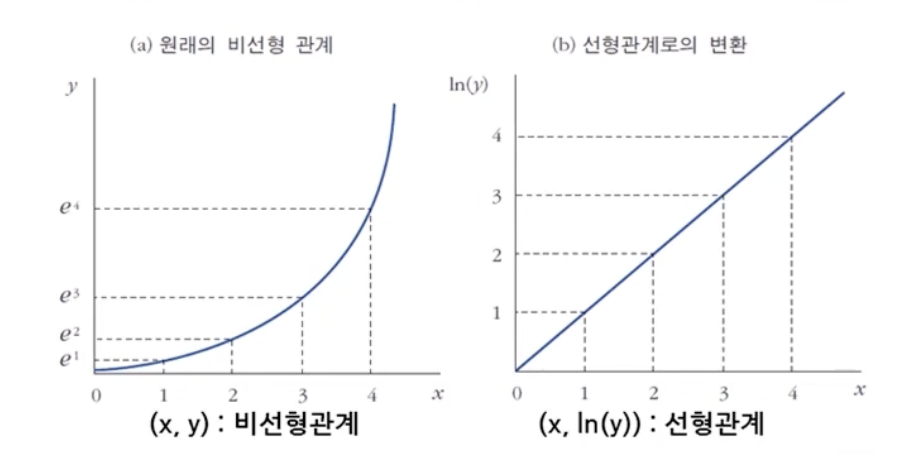
- 위처럼 곱으로 늘어나는 변수를 통계분석할 때는 보통 로그 변환을 통해 선형성을 만든다.
- 왜 로그변환을 취하여 선형성을 만드는지는 뒤로 좀 더 공부하다보면 알게 될것이다!!
- 선형성을 만드는건 중요!
linear spline equation
$ln(y)=12.78-0.0012x-0.0019(x-900)^+$
- (1) knots : 1개, x = 900 (매듭이 1개이고 위치가 x=900인 곳에 있다.
- (2) $x$, $(x-900)^+ = (음수면 0, 양수면 수식을 따른다)
중회귀 분석 (multiple regression analysis)
설명변수가 여러 개 있는 회귀분석
상관관계가 실제의 관계를 과장하는 경우
- 비율이나 평균의 자료로부터 구한 상관관계는 종종 실제의 관계를 과장
- 지역이나 국가 등 집단의 자료로부터 구한 상관계수는 개개인에게 적용되는 선형관계를 과장할 가능성이 있음
상관계수가 곧바로 인과관계는 아니다
- 자유무역과 경제성장
- 많은 연구에서 자유무역과 경제성장 간에는 양의 상관관계가 존재하는 것으로 나타난다. 과연 자유무역이 경제 성장의 원동력이라고 말할 수 있을까?
- 후진국 : 낙후된 지역, 잘못된 거시정책 (제3의 혼동요인 존재)
- 자본유입과 경제성장
- 중국 내 12개 성을 대상으로 조사한 결과 해외자본을 많이 유치한 성일수록 경제성장률이 높았다. 이 결과로부터 해외자본이 경제성장을 촉진시켰다고 말할 수 있을까?
- 해외투자자 : 성장잠재력이 큰 성에 투자할 것임 (역인과 관계 가능성)
'통계학' 카테고리의 다른 글
| 06. 회귀직선의 오차 RMSE (0) | 2025.03.14 |
|---|---|
| 05. 회귀분석 (0) | 2025.03.14 |
| 03. 정규분포로의 근사 (백분위수, 사분위수) (0) | 2025.03.10 |
| 02. 표준편차와 자유도 (1) | 2025.03.09 |