가장 간단한 관계가 직선이다
그렇게 상관계수와 상관관계를 배웠다
직선의 관계에 방향(기울기 양수,음수)이 있고, 강도(절대값 1에 가까울수록)가 있다
상관관계와 관련된 회귀직선을 공부하자!
regression line, regression equation
회귀분석
- 회귀분석(regression analysis)는 집단별 평균을 분석하는 통계적 방법
- 집단을 구분하는 분류지표가 한 개인지, 둘 또는 그 이상인지에따라 단순회귀분석과 중회귀분석으로 나누어짐
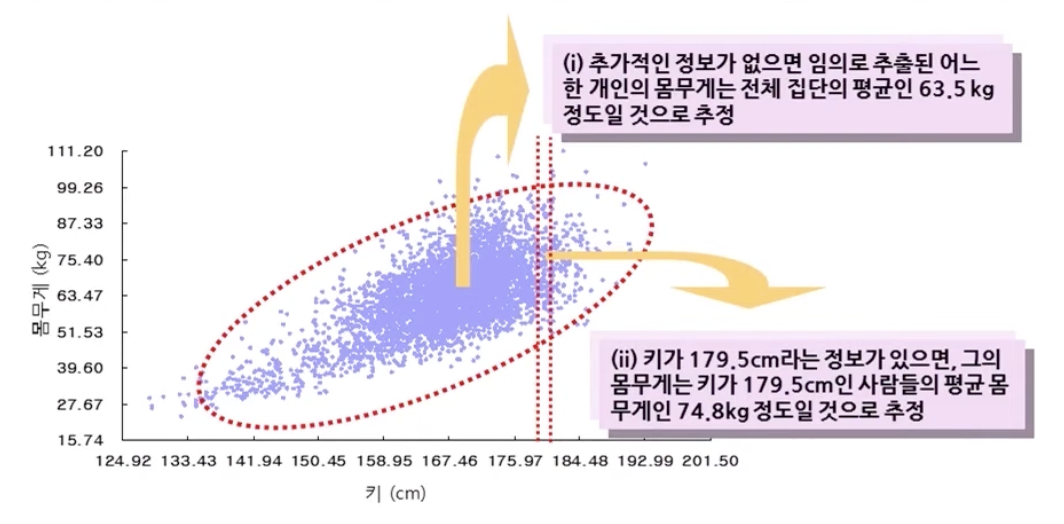
- 상관계수 = 0.67 : 키가 평균보다 $1SD_y$ 만큼 큰 사람들은 몸무게가 평균보다 대략 0.67$SD_y$ 만큼 더 나감
- 표준편차선 : 두 변수(여기서는 키와 몸무게)의 표준화된 변수 값이 같은 점들을 이은 직선
- 그렇다면 왜 회귀직선은 표준편차선보다 더 완만한가? 그 이유는 상관계수가 1이 아니기 때문!
- y의 x에 대한 회귀직선은 각각의 x에 대응하는 y의 평균값을 추정

- x 값이 x 평균값에서 $1SD_x$증가할 때 y값은 y평균값에서 $r x \times SD_y$
- r이 1이면 표준편차선이 되는 것!
- 회귀직선은 평균의 그래프를 하나의 직선으로 근사 시킨 것
- 평균의 그래프가 비선형이면 회귀직선으로의 선형 근사는 부적절
회귀분석 방법
- x의 표준편차가 한 단위 증가할 때, y는 y의 표준편차의 상관계수 배만큼 증가한다.
- x가 분류지표일 때, y를 x에 대하여 회귀분석 한다는 것은! x의 담긴 정보를 이용할 때 y 를 얼마나 직선으로 설명할 수 있는가
예: 경제학부 10학번 학생 100명을 대상으로 조사한 결과
경제원론 평균 = 3.0 표준편차($SD_x$) = 0.70
경제통계학 평균 = 3.0 표준편차($SD_y$) = 0.60
상관계수 = 0.5
문제 ) 경제원론 학점이 3.70인 지희의 경제통계학 학점은?
더보기
1. 경제원론 점수가 평균보다 (3.7-3)/0.7 = 1$SD_x$ 높으므로
2. 경제통계학 학점은 평균보다 $rSD_y$. 즉, 0.5 * 0.60 = 0.30 만큼 높을 것으로 예측
3. 따라서 경제통계학 학점의 예측치는 3.0 + 0.3 = 3.3 (B+) 이다.
평범으로의 회귀 (regression to mediocrity)

| ($x$) 중간고사 성적의 평균 | 129.3 |
| 표준편차 ($SD_x$) | 30.8 |
| ($y$) 기말고사 성적의 평균 | 112.4 |
| 표준편차($SD_y$) | 40.0 |
| 상관계수 | 0.64 |
- 중간고사에서 평균보다 높은 160점 받은 학생들의 기말소가 평균 점수는 138점으로 표준단위로 볼 때 하락했음
- 반면 중간고사에서 평균보다 낮은 110점 받은 학생들의 기말고사 평균 점수는 96.1점으로 표준단위로 볼 때 상승했음
회귀효과
- 회귀오류(regression fallacy)는 회귀효과를 무언가 중요한 효과로 착각하는 것
- 회귀효과의 배경
- (관찰된 점수) = (실제 실력) + (롹률오차)
- 예: 실제 실력은 평균 120, 표준편차 15의 정규분포를 따라 분포한다고 가정하자.
- 또 관측치에 든 확률오차는 각각 0.5의 확률로 $\pm5$라고 가정하자.
- 실제 실력이 135인 사람의 관찰된 점수는 각각 1/2의 확률로 130 또는 140
- 실제 실력이 145인 사람의 관찰된 점수는 각각 1/2의 확률로 140 또는 150
- 관찰된 점수로 140점 받은 사람의 경우 실제 실력은 135인데 확률오차가 +5인 경우가 실제 실력은 145인데 확률오차가 -5인 경우보다 더 가능성 높음 (평균이 120임을 참고!)
- 따라서 첫 번째 시험 점수가 평균보다 높으면, 아마도 실제 실력은 관찰된 점수보다 낮을 가능성이 큼
출처 : 류근관의 통계 특강 / 서울대학교 경제통계학 / 제10강 회귀분석
'통계학' 카테고리의 다른 글
| 07. 중회귀분석 (결정계수) (0) | 2025.03.17 |
|---|---|
| 06. 회귀직선의 오차 RMSE (0) | 2025.03.14 |
| 04. 상관관계와 회귀직선 (0) | 2025.03.12 |
| 03. 정규분포로의 근사 (백분위수, 사분위수) (0) | 2025.03.10 |